
SR and GR are abbreviations for special relativity and general relativity respectively. wdudvdw, we arrive, eventually, at the nal expression for the divergence in curvilinear coordinates replacing last quantity into formula (11): rv 1 h uh vh w (v uh vh w) u + (h uv vh w) v + (h uh vv w) w (15) From this last equation is also very immediate to derive the expression for the laplacian of a scalar eld ’. This article uses the (+ − − −) metric signature. 3.14 As a component of the RQM covariant derivative (internal particle spaces).3.13 As a key component in deriving quantum mechanics and relativistic quantum wave equations from special relativity.
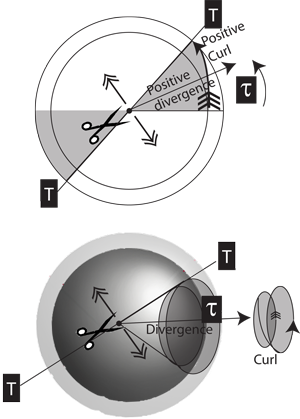
Freud (1939), permits a viable alternative to general relativity and a resolution of the 'field stress-energy' problem of the gravitational theory. 3.12 As a component of the wave equations and probability currents in relativistic quantum mechanics It is noted that the joint use of two basic differential identities in curved space-time, namely, 1) the Einstein-Hilbert identity (1915), and 2) the identity of P.Think of a curvy manifold M of dimension n each point p M has a unique vector space of dimension n tangent to p. 3.11 As a component of the covariant form of the quantum commutation relation The idea of a tangent space is very simple.3.10 As a component of the Schrödinger relations in quantum mechanics.3.9 As a component of the SR Hamilton–Jacobi equation in relativistic analytic mechanics 2 gives the Divergence Theorem in the plane, which states that the flux of a vector field across a closed curve equals the sum of the divergences over the.3.8 As a component of the 4D Gauss' Theorem / Stokes' Theorem / Divergence Theorem It has been shown that a fourdimensional spacetime with divergencefree Weyl conformal curvature tensor and admitting a proper conformal symmetry is.3.6 As a way to define the 4-wavevector.3.5 As a way to define the Faraday electromagnetic tensor and derive the Maxwell equations.3.4 As part of the total proper time derivative.3.3 As a way to define the Lorentz transformations.3.2 As a Jacobian matrix for the SR Minkowski metric tensor.3.1 As a 4-divergence and source of conservation laws.We prove that the resulting method converges with optimal order, is divergence-free, and is pressure-robust. In addition to defining curl and divergence, we look at some physical interpretations of them, and show their relationship to conservative and source-free vector fields. The velocity space has the same degrees of freedom as the quadratic Lagrange finite element space, and therefore the proposed spaces reduce to the Scott-Vogelius pair in the interior of the domain. For example, under certain conditions, a vector field is conservative if and only if its curl is zero. This integral is divergent and has to be regularized. We can also apply curl and divergence to other concepts we already explored. In QFT in curved space, one considers quantum matter fields in a classical gravity background. In addition, curl and divergence appear in mathematical descriptions of fluid mechanics, electromagnetism, and elasticity theory, which are important concepts in physics and engineering. They are important to the field of calculus for several reasons, including the use of curl and divergence to develop some higher-dimensional versions of the Fundamental Theorem of Calculus. In this section, we examine two important operations on a vector field: divergence and curl. Spontaneous symmetry breaking in curved space is shown to provide the induced gravity action with a cosmological constant. General considerations are followed by the formulation of scalar fields with non-minimal coupling. Use the properties of curl and divergence to determine whether a vector field is conservative. This chapter discusses classical fields in an arbitrary Riemann spacetime.Determine curl from the formula for a given vector field.Determine divergence from the formula for a given vector field.


 0 kommentar(er)
0 kommentar(er)
